In plants, this pattern begins within the apical dome. Each leaf starts as a primordium. As each primordium is initiated, the previous one is pushed farther out from the apex at nearly 137.5 degrees. The angle of divergence for the primordium is optimized when the spiraling sequence follows consecutive numbers from the Fibonacci Series. This means the plant can pack in the optimum number of primordia, allowing each equal space, without crowding. [Montgomery Botanical News 14 (2), p. 6.]With Tomlinson's image of Rhapis excelsa leaf primordia at the shoot apex (1990: Plate 8, p. 194), the angles of seven successive primordia were plotted using PhotoShop (ignoring the two initial very small primordia), numbered 1 the youngest, to 7, the oldest, as shown below. With one exception, 2 to 3 (c. 137.5°), these do not reflect the "Golden Angle" (137.58°). But the overall range is quite narrow. The average of all six angles is c. 146° — closely approximating the Fibonacci fraction 2/5 (0.4, 144°). The spiral appears to repeat itself (after 8 leaves) with the 6 to 7 angle, with light blue covering the angle plotted for 2 to 3 — and plotting 7 to 8 would seem to cover that for 3 to 4.

Tomlinson 1990, Plate 8. Rhapis excelsa. Transverse section of "crown at level of shoot apex to show progessive addition of leaf traces to shoot system." |
|
|---|---|
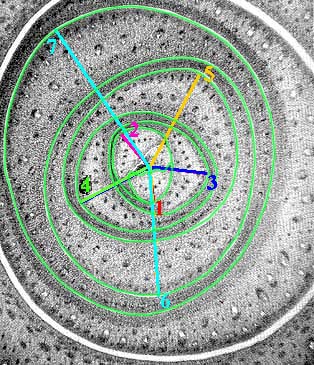
Angles of more clearly developed leaf primordia, numbered 1 to 7. |
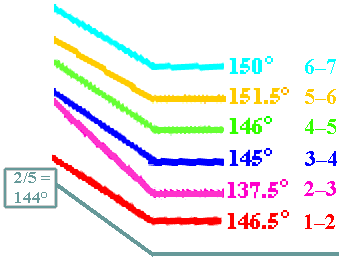
Angles from diagram on left, compared with Fibonacci fraction 2/5, 144° |
From Fig. 2.6 it is clear that the wedge shape of the leaves maximizes exposure efficiency, as does the relatively uniform radial distribution of leaves. The phyllotactic fraction, representing the primary leaf arrangement, is 3/8, a value which is closely approximated by the average angular divergence between successive leaves as measured in the crown projection, although the range is quite considerable. [p. 51]Tomlinson's leaves were color coded and their angles plotted as shown below:
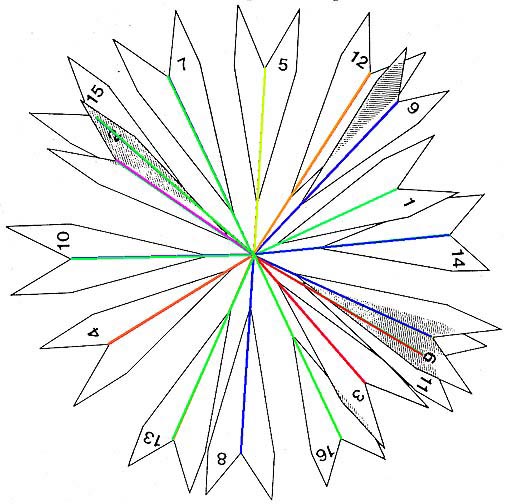
Fig. 2.6 with A. martiana leaf angles pairwise colored. |

Pairwise anticlockwise leaf angle sequences corresponding to those in Fig. 2.6; those with angles greater than 180° at the bottom. (A 135° angle, a phyllotactic 3/8 fraction, is also shown (gray). |
|---|
Tomlinson's A. martiana leaf crown seems to come no closer to his idealized 135° angle than did my Sabal minor to the Golden Angle. The above angles have been color coded to show their relationship to 135°. Those ±10° of the ideal are blue (only 4 of 15); those ±20°, green (5); those ±30°, violet (1); the two extremes (1–2, 261° & 11–12, 88°) are in red.
Although Tomlinson does note that "the range is quite considerable," I am left to wonder whether a 3/8 mathematical average provides a meaningful insight into the crown architecture of A. martiana.